nmöglichkeit  In der Schlauraffenzeit, da ging ich und sah, an einem kleinen Seidenfaden hing Rom und der Lateran, und ein fußloser Mann, der überlief ein schnelles Pferd, und ein bitterscharfes Schwert, das durchhieb eine Brücke. Da sah ich einen jungen Esel mit einer silbernen Nase, der jagte hinter zwei schnellen Hasen her, und eine Linde, die war breit, auf der wuchsen heiße Fladen. Da sah ich eine alte dürre Geiß, trug wohl hundert Fuder Schmalzes an ihrem Leibe und sechzig Fuder Salzes. Da sah ich zackern einen Pflug ohne Roß und Rinder, und ein jähriges Kind warf vier Mühlensteine von Regensburg bis nach Trier und von Trier hinein in Straßburg, und ein Habicht schwamm über den Rhein: das tat er mit vollem Recht. Da hört ich Fische miteinander Lärm anfangen, daß es in den Himmel hinaufscholl, und ein süßer Honig floß wie Wasser von einem tiefen Tal auf einen hohen Berg; das waren seltsame Geschichten. Da waren zwei Krähen, mähten eine Wiese, und ich sah zwei Mücken an einer Brücke bauen, und zwei Tauben zerrupften einen Wolf, zwei Kinder, die warfen zwei Zicklein, aber zwei Frösche droschen miteinander Getreid aus. Da sah ich zwei Mäuse einen Bischof weihen, zwei Katzen, die einem Bären die Zunge auskratzten. Da kam eine Schnecke gerannt und erschlug zwei wilde Löwen. Da stand ein Bartscherer, schor einer Frauen ihren Bart ab, und zwei säugende Kinder hießen ihre Mutter stillschweigen. Da sah ich zwei Windhunde, brachten eine Mühle aus dem Wasser getragen, und eine alte Schindmähre stand dabei, die sprach, es wäre recht. Und im Hof standen vier Rosse, die droschen Korn aus allen Kräften, und zwei Ziegen, die den Ofen heizten, und eine rote Kuh schoß das Brot in den Ofen.  - (grim)

Unmöglichkeit ⁽²⁾  Wir gehen natürlich nicht von der Vorstellung aus, daß der Mensch 1000 Jahre leben kann. Den Formeln zufolge, die aus heutigen Sterbetafeln hergeleitet wurden, ist der Anteil der Menschen, die 1000 Jahre leben könnten, gleich eins, dividiert durch eine Zahl, bestehend aus einer Eins mit dreihundertsechzig Nullen. Die Behauptung, ein Mensch könne ein solches Alter erreichen, ist aus biologischer Sicht unhaltbar, aber wenn sie rein statistisch betrachtet wird, so steht diese Behauptung nicht im Widerspruch zum Versuch. In einem Jahrhundert werden höchstens 10 Milliarden Menschen geboren, und um die obige Behauptung statistisch zu widerlegen, wären 10350 Jahrhunderte erforderlich. Dies übersteigt das Alter der Erde um das 10340fache. Offensichtlich muß man für so kleine Wahrscheinlichkeiten unseren Begriff der Unmöglichkeit verwenden. - Vladimir Petrovic Karcev und Petr Michailovic Chazanovskij, Warum irrten die Experten? Unglücksfälle und Katastrophen aus der Sicht rechnischer Zuverlässigkeit. Berlin 1990 (zuerst 1980)

Unmöglichkeit ⁽³⁾  Man muss das Unmögliche so lange anschauen, bis es eine leichte Angelegenheit ist. - (beb)

Unmöglichkeit ⁽⁴⁾  Jeder, der über den Kreis des Unmöglichen hinausgehen möchte, wird dabei seinen Verstand verlieren.   - Bousquet, nach (lim)

Unmöglichkeit ⁽⁵⁾  Auch wenn manche gern sagen, nichts sei unmöglich, kennt man in den Wissenschaften doch mancherlei Unmögliches, und sei es auch nur dadurch bedingt, dass jede Wissenschaft ihren Gegenstandsbereich präzise abgrenzen muss. Da Wissenschaften niemals synkretistisch sein können (das heißt die Gesamtheit des Wissens über die Gesamtheit aller Objekte in sich vereinigen), bestimmen sie durch die Abgrenzung ihres Gegenstandsbereiches stets auch jenen Bereich, über den sie mit ihren Methoden unmöglich etwas auszusagen vermögen. Hierher gehören zum Beispiel alle Fragen, die den Ursprung der Dinge betreffen.  - (thes)

Unmöglichkeit ⁽⁶⁾  Man weiß zum Beispiel, dass die Quadratur des Kreises unmöglich ist. Die Quadratur des Kreises bestünde darin, mit Zirkel und Lineal zu einem Kreis beliebiger Größe ein flächengleiches Rechteck oder Quadrat zu konstruieren oder, was auf dasselbe hinausliefe, eine Sehne der Länge 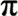einzuzeichnen. Diese Behauptung basiert auf einem Satz, den Pierre Wantzel 1837 bewiesen hat, wonach die Länge aller mit Zirkel und Lineal konstruierten Sehnen einer algebraischen Zahl entspricht, das heißt der Lösung einer algebraischen Gleichung mit ganzzahligen Koeffizienten.

Der Mathematiker Ferdinand von Lindemann bewies dann 1882, dass die Zahl 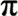 keine algebraische Zahl ist. Damit war das Problem gelöst oder besser gesagt, es war bewiesen, dass es keine Lösung gibt.   - (thes)

Unmglichkeit ⁽⁷⁾  Komische Träume in letzter Zeit: Bubis Geburtstag, er klagt über Zähne. Ich schau ihm in S' den Mund und sehe hinter jedem Zahn ein winziges Froschköpfchen. Mir wird ganz kalt vor Schreck, und ich denke: „Hab ich ihn denn so vernachlässigt?" Mit ihm zum Doktor, und der sagte: „Oh, das kommt schon vor, besonders bei Kindern." Dann zeigte er mir drei Wespen, die er eingesperrt hatte, und ein kleines Stück grünes Tuch. Erzählte: „Sehn Sie, das haben die Wespen mir gefärbt." Ich sollte draus sehn, daß Unmögliches möglich wäre, sah es auch ein und war ganz befriedigt.  - Franziska Gräfin zu Reventlow, nach (je)